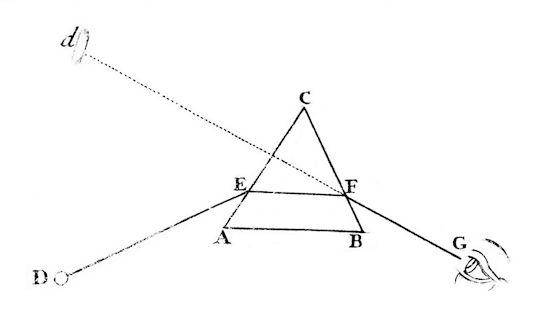
During the Exploration, students take part in an experience that provides "a common base of activities within which current concepts (i.e., misconceptions), processes, and skills are identified and conceptual change is facilitated. Learners may complete lab activities that help them use prior knowledge to generate new ideas, explore questions and possibilities, and design and conduct a preliminary investigation” (Bybee et a. 2006, p. 2).
History can provide ideas for how to structure an effective exploration. The questions faced by real mathematicians and scientists of earlier eras can provide teachers with a framework of “big idea” conceptual questions around which to focus student activities. This can be especially effective, because students may hold preconceptions comparable to those held by people in the past. Real-life puzzles from history can also provide students with compelling contexts for exploring science and math concepts, while at the same time laying the groundwork for teaching the nature of science and math.